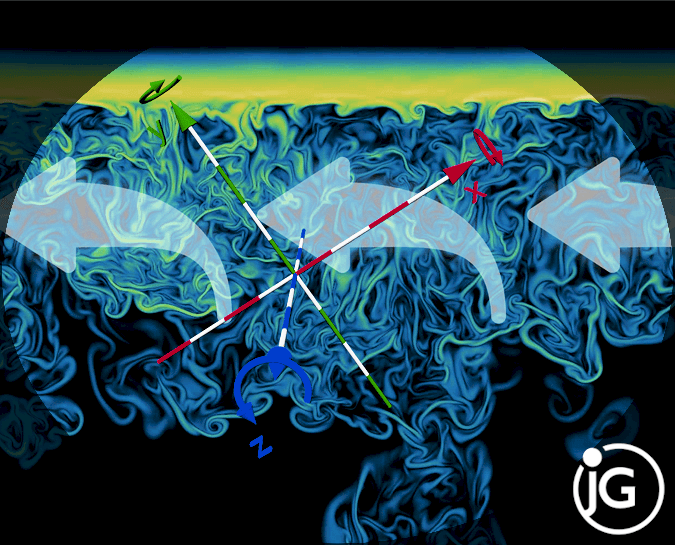
Modeling of uniform rotation effects on homogeneous decaying turbulence
Article Sidebar

Vols. 1-18 (1924-1944), ISSN 0044-2801
Main Article Content
Abstract
Hydrodynamic turbulence under rotation is often encountered in geophysics and astrophysics, inspiring extensive research into the effects of rotation on turbulence. Amongst numerous scenarios in those studies, the rotating homogeneous decaying turbulence stands out as a canonical case study of turbulence theory. I report a physical 2nd-order closure model to simulate homogeneous decaying turbulence under uniform rotation, which corrects a previous solution. The rotation effects are functions of the rotation rate Ω, the parallel component of the Reynolds stress tensor, and the integral length scale along the rotation axis, together with its isotropic value. The results demonstrate that the new remedying model effectively reproduces theoretical predictions, aligning closely with data from direct numerical simulations and outperforming old physical models from the same class.
 ARK: https://n2t.net/ark:/88439/x071373
ARK: https://n2t.net/ark:/88439/x071373
Permalink: https://geophysicsjournal.com/article/361
Article Details
References
Bartello, P., Metais, O., Lisieur, M. (1994) Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273:1–29. https://doi.org/10.1017/S0022112094001837
Bartoud, N., Plapp, B., She, Z., Swinney, L. (2002) Anomalous self-similarity in a turbulent rapidly rotating fluid. Phys. Rev. Lett. 88:114501. https://doi.org/10.1103/PhysRevLett.88.114501
Cambon, C., Mansour, N., Godeferd, S. (1997) Energy transfer in rotating turbulence. J. Fluid. Mech. 337:303–332. https://doi.org/10.1017/S002211209700493X
Davidson, P.A. (2010) On the decay of Saffman turbulence subjected to rotation, stratification or an imposed magnetic field. J. Fluid Mech. 663:268–292. https://doi.org/10.1017/S0022112010003496
Deming, N., Jianzhong, L., Limin, Q. (2013) Direct numerical simulations of the decaying turbulence in rotating flows via the MRT-lattice Boltzmann method. Int. J. Comp. Fluid Dyn. 27:173–183. https://doi.org/10.1080/10618562.2013.779679
Fu, S., Launder, B., Tselepidakis, D. (1987) Accommodating the effects of high strain rates in modelling the pressure-strain correlation. UMIST Mech. Engr. Dept. Rep. TFD/87/5.
Gatski, B., Speziale, C.G. (1993) On explicit algebraic stress models for complex turbulent flows. J. Fluid Mech. 254:59–78. https://doi.org/10.1017/S0022112093002034
Hanjalić, K., Launder, B. (1980) Sensitizing the dissipation equation to irrotational strains. ASME J. Fluids Eng. 102:34–40. https://doi.org/10.1115/1.3240621
Haworth, C., Pope, B. (1986) A generalized Langevin model for turbulent flows. Phys. Fluids 29:387–405. https://doi.org/10.1063/1.865723
Huidan, Y., Grimaji, S., Luo, S. (2005) DNS and LES of decaying isotropic turbulence with and without frame rotation using lattice Boltzmann method. J. Comput. Phys. 209:599–616. https://doi.org/10.1016/j.jcp.2005.03.022
Jacquin, L., Leuchter, O., Cambon, C., Mathieu, J. (1990) Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220:1–52. https://doi.org/10.1017/S0022112090003172
Launder, B., Reece, G.W., Rodi, W. (1975) Progress in the development of a Reynolds stress turbulence closure. J. Fluid Mech. 68:537–566. https://doi.org/10.1017/S0022112075001814
Launder, B., Spalding, D. (1974) The numerical Computation of turbulent flows. Comput. Methods Appl. Mech. Engr. 3:269–289. https://doi.org/10.1016/0045-7825(74)90029-2
Mahalov, A., Zhou, Y. (1996) Analytical and phenomenological studies of rotating turbulence. Phys. Fluids 8:2138–2152. https://doi.org/10.1063/1.868988
Mansour, N., Cambon, C., Speziale, C.G. (1991) Single point modeling of initially isotropic turbulence under uniform rotation. Center for Turbulence Research, Stanford University, Ann. Res. Briefs p.159. https://ui.adsabs.harvard.edu/abs/1991arb..nasa..159M
Marzougui, H. (2016) K – ∈ model for rotating homogeneous decaying turbulence. Can. J. Phys. 94(11):1200–1204. https://doi.org/10.1139/cjp-2016-0543
Morinishi, Y., Nakabayashi, K., Ren, S. (2001b) Dynamics of anisotropy on decaying homogeneous turbulence subjected to system rotation. Phys. Fluids 13:2912–2922. https://doi.org/10.1063/1.1398040
Morinishi, Y., Nakabayashi, K., Ren, S. (2001a) A new DNS algorithm for rotating homogeneous decaying turbulence. Int. J. Heat Fluid Flow 22:30–38. https://doi.org/10.1016/S0142-727X(00)00067-9
Okamoto, M. (1995) Theoretical turbulence modelling of homogeneous decaying flow in a rotating frame. J. Phys. Soc. Japan 64:2854–2867. https://doi.org/10.1143/JPSJ.64.2854
Park, J., Chung, M. (1999) A model for the decay of rotating homogeneous turbulence. Phys. Fluids. 11:1544–1549. https://doi.org/10.1063/1.870017
Pope, S. (1978) An explanation of the turbulent round jet/plane jet anomaly. AIAA J. 16(3):279–281. https://doi.org/10.2514/3.7521
Raj, R. (1975) Form of the turbulence dissipation equation as applied to curved and rotating turbulent flows. Phys. Fluids. 18:1241–1244. https://doi.org/10.1063/1.861008
Ristorcelli, R. (1996) Toward a turbulence constitutive relation for rotating flows. NASA Contractor Report 201621. https://ntrs.nasa.gov/api/citations/19970004242/downloads/19970004242.pdf
Shih, T.-H., Lumley, J. (1985) Modeling of pressure correlation terms in Reynolds stress and scalar flux equations. Sibley School of Mechanical and Equations Aerospace Engineering, Cornell University Tech. Rep. FDA 85(3).
Shimomura, Y. (1993) Turbulence modelling suggested by system rotation, in Near-wall turbulent flows. Edited by So, R.M.C., Speziale, C.G., Launder, B., Elsevier Science, Amsterdam. ISBN 0444896635. https://www.researchgate.net/publication/275213056_Near-Wall_Turbulent_Flows
Speziale, C.G. (1989) Turbulence modelling in non-inertial frames of reference. Theor. Comput. Fluid Dyn. 1:3–19. https://doi.org/10.1007/BF00271419
Speziale, C.G. (1985) Second-order closure models for rotating turbulent flows. Icase report N085-49. https://ntrs.nasa.gov/citations/19860007047
Speziale, C.G., Gatski, T., Mhuiris, N. (1990) A critical comparison of turbulence models for homogeneous shear flows in a rotating frame. Phys. Fluids 2:1678 –1684. https://doi.org/10.1063/1.857575
Speziale, C.G., Mansour, N., Rogallo, S. (1987) The decay of isotropic turbulence in a rapidly rotating frame. Proc. the 1987 Summer Program, Center of Turbulence Research, Stanford University & NASA Ames Research Center. https://ntrs.nasa.gov/citations/19880013723
Speziale, C.G., Raj, R., Gatski, B. (1990) Modeling the dissipation rate in rotating turbulent flows. Icase Report No. 90-88. https://ntrs.nasa.gov/citations/19910006993
Speziale, C.G., Sarkar, S., Gatski, B. (1991) Modelling the pressure-strain correlation of turbulence: an invariant dynamical systems approach. J. Fluid. Mech. 227:245–272. https://doi.org/10.1017/S0022112091000101
Vorobev, A., Zikanov, O., Davidson, P., Knaepen, B. (2005) Anisotropy of magnetohydrodynamic turbulence at low magnetic Reynolds number. Phys. Fluids 17:125105. https://doi.org/10.1063/1.2140847
Yang, X., Domaradzki, J. (2004) Large eddy simulations of decaying rotating turbulence. Phys. Fluids 16:4088–4104. https://doi.org/10.1063/1.1790452
Yeung, K., Zhou, Y (1998) Numerical study of rotating turbulence with external forcing. Phys. Fluids 10:2895–2909. https://doi.org/10.1063/1.869810
Zeman, O. (1994) A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 6:3221–3223. https://doi.org/10.1063/1.868053
Zhou, Y. (1995) A phenomenological treatment of rotating turbulence. Phys. Fluids 7:2092–2094. https://doi.org/10.1063/1.868457