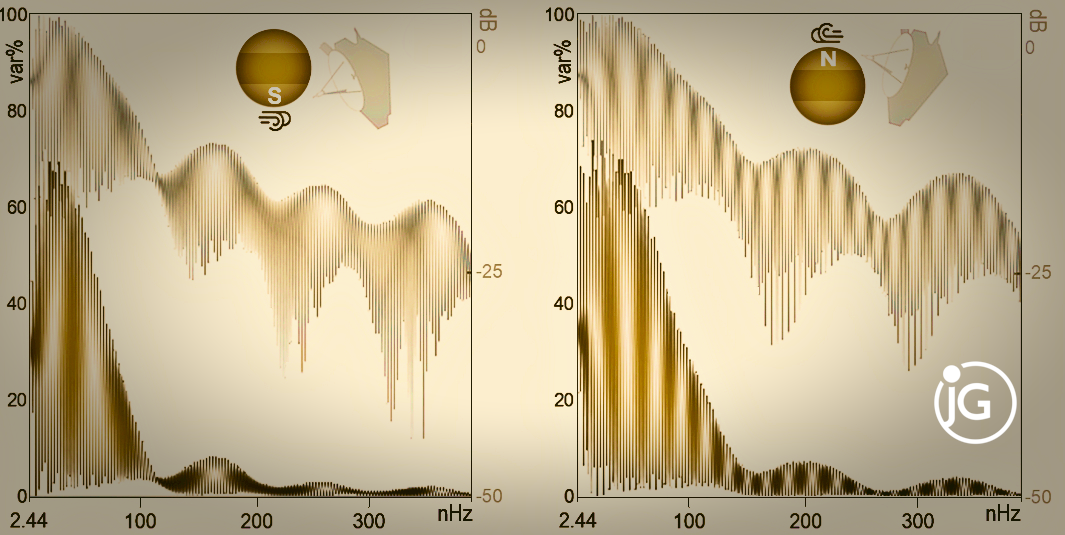
The Sun as a revolving-field magnetic alternator with a wobbling-core rotator from real data
Ulysses replaces dynamo with magnetic alternator in our Sun and Sun-like stars
Article Sidebar

Vols. 1-18 (1924-1944), ISSN 0044-2801
Main Article Content
Abstract
Rather than as a star classically assumed to feature elusive dynamo or a proverbial engine and impulsively alternating polarity, the Sun reveals itself in the 385.8–2.439-nHz (1-month–13-years) band of polar (φSun>|70°|) wind’s decadal dynamics, dominated by the fast (>700 km s−1) winds, as a globally completely vibrating revolving-field magnetic alternator at work at all times. Thus North–South separation of 1994–2008 Ulysses in situ <10nT polar-wind samplings reveals Gauss–Vaníček spectral signatures of an entirely ≥99%-significant, Sun-borne global incessant sharp Alfvén resonance (AR), Pi=PS/i, i=2…n, i∈ℤ ∧ n∈א, accompanied by a symmetrical sharp antiresonance P-. The ideal Sun (slow winds absent) AR imprints to the order u=136 into the fast winds nearly theoretically, with the northerly winds preferentially more so. The spectral peaks’ fidelity is very high (≫12) to high (>12) and reaches Φ>2∙103, validating the signatures as a global dynamical process. The fast-wind spectra reveal upward drifting low-frequency trends due to a rigid core and undertones due to a core offset away from the apex. While the consequent core wobble with a 2.2±0.1-yr return period is the AR trigger, the core offset causes northerly preferentiality of Sun magnetism. Multiple total (band-wide) spectral symmetries of solar activity represented by historical solar-cycle lengths and sunspot and calcium numbers expose the solar alternator and core wobble as the moderators of sunspots, nanoflares, and coronal mass ejections that resemble machinery sparking. The real Sun (slow winds inclusive) AR resolves to n=100+ and is governed by the PS=~11-yr Schwabe global damping (equilibrium) mode northside, its ~10-yr degeneration equatorially, and ~9-yr southside. The Sun is a typical ~3-dB-attenuated ring system, akin to rotating machinery with a wobbling rotator (core), featuring differentially revolving and contrarily (out-of-phase-) vibrating conveyor belts and layers, as well as a continuous global spectrum with patterns complete in both parities and the >81.3 nHz(S) and 55.6 nHz(N) resolution in lowermost frequencies (≲2 μHz in most modes). The global decadal vibration resonantly (quasi-periodically) flips the core, thus alternating the magnetic polarity of our host star. Unlike a resonating motor restrained from separating its casing, the cageless Sun lacks a stator and vibrates freely, resulting in all-spin and mass release (fast solar winds) in an axial shake-off beyond L1 at discrete wave modes generated highly coherently by the whole Sun. Thus, the northerly and southerly antiresonance tailing harmonic P-17 is the well-known PRg=154-day (or PS/3/3/3 to ±1‰) Rieger period from which the wind’s folded Rieger resonance (RR) sprouts, governing solar-system (including planetary) dynamics and space weather. AR and its causes were verified against remote data and the experiment, thus instantly replacing the dynamo with a magnetoalternator and advancing basic knowledge on the >100 billion trillions of solar-type stars. Shannon’s theory-based Gauss-Vanicek spectral analysis revolutionizes astrophysics and space science by rigorously simulating fleet formations from a single spacecraft and physics by computing nonlinear global dynamics directly (rendering spherical approximation obsolete).
 ARK: https://n2t.net/ark:/88439/x080008
ARK: https://n2t.net/ark:/88439/x080008
Permalink: https://geophysicsjournal.com/article/320

News Feature (2023) Two centuries-long mystery solved: the Sun acts as a magnetic alternator, not dynamo. J. Geophys. 65(1):78-79

Global coupling mechanism of Sun resonant forcing of Mars, Moon, and Earth seismicity. J. Geophys. 65(1):1-46
 Read the press release for this article
Read the press release for this article
Article Details
References
Alfvén, H. (1948) Cosmical electrodynamics. Oxford University Press (2nd ed. Clarendon Press, 1963), 228 pp. ISBN 9780198512011
Alfvén, H. (1943) On Sunspots and the Solar Cycle. Arkiv f. Mat., Astron. o. Fys. 29A(12):1–17. https://ui.adsabs.harvard.edu/abs/1943ArMAF..29R...1A
Alfvén, H. (1942) Existence of electromagnetic-hydrodynamic waves. Nature 150(3805):405–406. https://doi.org/10.1038%2F150405d0
An, Y., Ding, H., Chen, Z. et al. (2023) Inner core static tilt inferred from intradecadal oscillation in the Earth’s rotation. Nat. Commun. 14:8130. https://doi.org/10.1038/s41467-023-43894-9
Asplund, M., Grevesse, N., Sauval, A.J., Scott, P. (2009) The chemical composition of the Sun. Ann. Rev. Astron. Astrophys. 47(1):481–522. https://doi.org/10.1146/annurev.astro.46.060407.145222
Bai T. and Cliver E. W. (1990) A 154 day periodicity in the occurrence rate of proton flares. Astrophys. J. 363:299–309. https://doi.org/10.1086/169342
Balogh, A. (1988) The Ulysses magnetometer. In: IEEE Colloquium on Satellite Instrumentation, 20 January, London, United Kingdom. Institution of Engineering and Technology. https://ieeexplore.ieee.org/xpl/conhome/2179/proceeding
Bellan, P.M. (1996) Mode conversion into non-MHD waves at the Alfvén layer: The case against the field line resonance concept. J. Geophys. Res. 101(A11):24887–24898. https://doi.org/10.1029/96JA02253
Bellan, P.M. (1994) Alfvén ‘resonance’ reconsidered: Exact equations for wave propagation across a cold inhomogeneous plasma. Phys. Plasmas 1:3523–3541. https://doi.org/10.1063/1.870888
Bergemann M., Serenelli A. (2014) Solar Abundance Problem. In: Niemczura E., Smalley B., Pych W. (Eds.) Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars. GeoPlanet: Earth and Planetary Sciences. Springer. https://doi.org/10.1007/978-3-319-06956-2_21
Borovsky, J.E. (2018) The spatial structure of the oncoming solar wind at Earth and the shortcomings of a solar-wind monitor at L1. J. Atmo. Solar-Terr. Phys. 177:2-11. https://doi.org/10.1016/j.jastp.2017.03.014
Bose, S., Nagaraju, K. (2018) On the variability of the Solar Mean Magnetic Field: contributions from various magnetic features on the surface of the Sun. Astrophys. J. 862:35. https://doi.org/10.3847/1538-4357/aaccf1
Brooks, D., Ugarte-Urra, I., Warren, H. (2015) Full-Sun observations for identifying the source of the slow solar wind. Nat. Commun. 6:5947. https://doi.org/10.1038/ncomms6947
Brown, B. (2011) Dynamos in Stellar Convection Zones: of Wreaths and Cycles. J. Phys.: Conf. Ser. 271:012064. https://doi.org/10.1088/1742-6596/271/1/012064
Bruno, R., Carbone, V. (2013) The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10:2. https://doi.org/10.12942/lrsp-2013-2
Campos, L. (1977) On the generation and radiation of magneto-acoustic waves. J. Fluid Mech. 81(3):529–549. https://doi.org/10.1017/S0022112077002213
Cane, H.V., Richardson, I.G., von Rosenvinge, T.T. (1998) Interplanetary magnetic field periodicity of ∼153 days. Geophys. Res. Lett. 25(24):4437–4440. https://doi.org/10.1029/1998GL900208
Carbonell, M., Oliver, R., Ballester, J.L. (1992) Power spectra of gapped time series: a comparison of several methods. Astron. & Astrophys. 264:350–360. https://ui.adsabs.harvard.edu/#abs/1992A&A...264..350C
Choi, K.-E., Lee, D.-Y. (2019) Origin of solar rotational periodicity and harmonics identified in the Interplanetary Magnetic Field Bz component near the Earth during solar cycles 23 and 24. Sol. Phys. 294:44. https://doi.org/10.1007/s11207-019-1433-7
Cole, M.O.T (2008) On stability of rotordynamic systems with rotor–stator contact interaction. Proc. R. Soc. A. 4643353–3375. https://doi.org/10.1098/rspa.2008.0237
Craymer, M.R. (1998) The Least Squares Spectrum, Its Inverse Transform and Autocorrelation Function: Theory and Some Applications in Geodesy. Ph.D. Dissertation, University of Toronto, Canada. https://hdl.handle.net/1807/12263
Crossley, D.J., Rochester, M.G. (1980) Simple core undertones. Geophys. J. Int. 60(2):129–161. https://doi.org/10.1111/j.1365-246X.1980.tb04287.x
Czech, M.J., Thomas, R.H. (2013) Open Rotor Aeroacoustic Installation Effects for Conventional and Unconventional Airframes. 19th AIAA/CEAS Aeroacoustics Conference, Berlin Germany, 27-29 May. American Institute of Aeronautics and Astronautics. https://ntrs.nasa.gov/citations/20130013993
Danilović, S., Vince, I., Vitas, N., Jovanović, P. (2005) Time series analysis of long term full disk observations of the Mn I 539.4 nm solar line. Serb. Astron. J. 170:79–88. https://doi.org/10.2298/SAJ0570079D
Davila, J.M. (1987) Heating of the solar corona by the resonant absorption of Alfven waves. Astrophys. J. 317:514–521. https://ui.adsabs.harvard.edu/#abs/1987ApJ...317..514D
Den Hartog, J.P. (1985) Mechanical Vibrations. Dover Publications, New York, United States. ISBN 0486647854
Deng, L.H. Li, B., Xiang, Y.Y., Dun, G.T. (2014) On mid-term periodicities of high-latitude solar activity. Adv. Space Res. 54(1):125–131. https://doi.org/10.1016/j.asr.2014.03.006
Deubner, F.-L., Gough, D. (1984) Helioseismology: Oscillations as a Diagnostic of the Solar Interior. Ann. Rev. Astron. Astrophys. 22(1):593–619. https://doi.org/10.1146/annurev.aa.22.090184.003113
Dimitropoulou, M., Moussas, X., Strintzi, D. (2008) Enhanced Rieger type periodicities' detection in X-ray solar flares and statistical validation of Rossby waves' existence. Proc. Int. Astron. Union 4(S257):159–163. https://doi.org/10.1017/S1743921309029226
Dzhalilov, N.S., Staude, J., Oraevsky, V.N. (2002) Eigenoscillations of the differentially rotating Sun — I. 22-year, 4000-year, and quasi-biennial modes. Astron. Astrophys. 384(1):282–298. https://doi.org/10.1051/0004-6361:20011836
Ewins, D.J. (1995) Modal Testing: Theory and Practice. Research Studies Press Ltd., Taunton, England, ISBN 0863800173. John Wiley & Sons lnc., ISBN 04719904724. 313 pp.
Forgacs-Dajka, E., Borkovits, T. (2007) Searching for mid-term variations in different aspects of solar activity – looking for probable common origins and studying temporal variations of magnetic polarities. Mon. Not. R. Astron. Soc. 374:282–291. https://doi.org/doi:10.1111/j.1365-2966.2006.11167.x
Fossat, E., Boumier, P., Corbard, T., Provost, J., Salabert, D., et al. (2017) Asymptotic g modes: Evidence for a rapid rotation of the solar core. Astron. Astrophys. 604:A40. https://doi.org/10.1051/0004-6361/201730460
Goedbloed, J.P., Lifschitz, A. (1995) Comment on "Alfvén ‘resonance’ reconsidered: Exact equations for wave propagation across a cold inhomogeneous plasma" [Phys. Plasmas 1:3523 (1994)]. Phys. Plasmas 2:3550–3551. https://doi.org/10.1063/1.871471
Gough, D. (1995) Waves in the wind. Nature 376:120–121. https://doi.org/10.1038/376120a0
Grail, R., Coles, W., Klinglesmith, M., Breen, A.R., Williams, P.J.S., et al. (1996) Rapid acceleration of the polar solar wind. Nature 379:429–432. https://doi.org/10.1038/379429a0
Grant, S.D.T., Jess, D.B., Zaqarashvili, T.V. Beck, C., Socas-Navarro, H., et al. (2018) Alfvén wave dissipation in the solar chromosphere. Nature Phys. 14:480–483. https://doi.org/10.1038/s41567-018-0058-3
Grote, E., Busse, F.H. (2000) Hemispherical dynamos generated by convection in rotating spherical shells. Phys. Rev. E 62:4457–4460. https://doi.org/10.1103/PhysRevE.62.4457
Gurgenashvili, E., Zaqarashvili, T.V., Kukhianidze, V., Oliver, R., Ballester, J.L., et al. (2017) North–South Asymmetry in Rieger-type Periodicity during Solar Cycles 19–23. Astrophys. J. 845(2):137–148. https://dx.doi.org/10.3847/1538-4357/aa830a
Gurgenashvili, E., Zaqarashvili, T.V., Kukhianidze, V., Oliver, R., Ballester, J.L., et al. (2016) Rieger-type periodicity during solar cycles 14–24: estimation of dynamo magnetic field strength in the solar interior. Astrophys. J. 826(1):55. https://doi.org/10.3847/0004-637X/826/1/55
Hagedorn, P., Eckstein, M., Heffel, E., and Wagner, A. (2014) Self-Excited Vibrations and Damping in Circulatory Systems. ASME. J. Appl. Mech. 81(10):101009. https://doi.org/10.1115/1.4028240
Hellevik, K., Gudmestad, O.T. (2017) Limit cycle oscillations at resonances. IOP Conf. Ser.: Mater. Sci. Eng. 276:012020. https://doi.org/10.1088/1757-899X/276/1/012020
He, J., Fu, Z.-F. (2001) Modal Analysis. Butterworth-Heinemann. ISBN 9780750650793. https://doi.org/10.1016/B978-0-7506-5079-3.X5000-1
Jones, G., Balogh, A. (2003) The global heliospheric magnetic field polarity distribution as seen at Ulysses. Annales Geophysicae 21(6):1377–1382. https://doi.org/10.5194/angeo-21-1377-2003
Kasper, J.C., Maruca, B.A., Stevens, M.L., Zaslavsky, A. (2013) Sensitive Test for Ion-Cyclotron Resonant Heating in the Solar Wind. Phys. Rev. Lett. 110:091102. https://doi.org/10.1103/PhysRevLett.110.091102
Kim, C.-H., Ih, J.-G. (2007) On the horizontal wobbling of an object levitated by near-field acoustic levitation. Ultrasonics 46(4):331-335. https://doi.org/10.1016/j.ultras.2007.05.001
Kinkhabwala, A. (2013) Maximum Fidelity. Max Planck Institute of Molecular Physiology report. arXiv:1301.5186, Subject: Statistics Theory (math.ST). https://doi.org/10.48550/arXiv.1301.5186
Knaack, R., Stenflo, J.O. (2005) Spherical harmonic decomposition of solar magnetic fields. Astron. Astrophys. 438(1):349–363. https://doi.org/10.1051/0004-6361:20052765
Kurochkin, N.E. (1998) Transient periodicity in solar activity. Astron. Astrophys. Trans. 15(1–4):277–279. https://doi.org/10.1080/10556799808201781
Li, H., Wang, C., Richardson, J.D. (2008) Properties of the termination shock observed by Voyager 2. Geophys. Res. Lett. 35:L19107. https://doi.org/10.1029/2008GL034869
Markovskii, S.A., Vasquez, B.J., Hollweg, J.V. (2009) Proton heating by nonlinear field-aligned Alfvén waves in solar coronal holes. Astrophys. J. 695(2):1413. https://doi.org/10.1088/0004-637X/695/2/1413
Mattsson, L., Wahlin, R., Höfner, S. (2010) Dust driven mass loss from carbon stars as a function of stellar parameters — I. A grid of solar-metallicity wind models. Astron. Astrophys. 509:A14. https://doi.org/10.1051/0004-6361/200912084
McLeod, A.F., Dale, J.E., Evans, C.J., Ginsburg, A., Kruijssen, J.M.D., et al. (2019) Feedback from massive stars at low metallicities: MUSE observations of N44 and N180 in the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 486:5263–5288. https://doi.org/10.1093/mnras/sty2696
Miller, J.A., Ramaty, R. (1989) Relativistic Electron Transport and Bremsstrahlung Production in Solar Flares. Astrophys. J. 344:973. https://doi.org/10.1086/167865
Omerbashich, M. (2023a) Earth as a time crystal: macroscopic nature of a quantum-scale phenomenon exposes quantum physics as tidally-resonantly localized to host star. arXiv:2301.02578, Subject: Geophysics (physics.geo-ph); Quantum Physics (quant-ph). https://doi.org/10.48550/arXiv.2301.02578
Omerbashich, M. (2023b) Global coupling mechanism of Sun resonant forcing of Mars, Moon, and Earth seismicity. J. Geoph. 65(1):1–46. https://n2t.net/ark:/88439/x040901
(PR: https://www.openpr.com/news/2982920/scientists-now-know-that-and-how-the-sun-paces-strong-quakes )
Omerbashich, M. (2023c). Jovian pulsars — a new class of pulsars from a magnetar- & dwarf novae-type prebursting evolution of Jupiter's global decadal magnetoactivity since 1996. Zenodo. https://doi.org/10.5281/zenodo.8231607
Omerbashich, M. (2022) Non-marine tetrapod extinctions solve extinction periodicity mystery. Hist. Biol. 34(1):188-191. https://doi.org/10.1080/08912963.2021.1907367
Omerbashich, M. (2007) Magnification of mantle resonance as a cause of tectonics. Geodinamica Acta 20:6:369–383. https://doi.org/10.3166/ga.20.369-383
Omerbashich, M. (2006) Gauss–Vaníček Spectral Analysis of the Sepkoski Compendium: No New Life Cycles. Comp. Sci. Eng. 8(4):26–30. https://doi.org/10.1109/MCSE.2006.68 (Omerbashich, M. (2007) Erratum due to journal error. https://doi.org/10.1109/MCSE.2007.79; full text: https://arxiv.org/abs/math-ph/0608014; Comp. Sci. Eng. 9(4):5–6.)
Omerbashich, M. (2003) Earth-model Discrimination Method. Ph.D. Dissertation, pp.129. Department of Geodesy, University of New Brunswick, Canada. ProQuest, USA. https://doi.org/10.6084/m9.figshare.12847304
Pagiatakis, S. (1999) Stochastic significance of peaks in the least-squares spectrum. J. Geod. 73:67–78. https://doi.org/10.1007/s001900050220
Pap, J., Tobiska, W.K., Bouwer, S.D. (1990) Periodicities of solar irradiance and solar activity indices, I. Sol. Phys. 129:165–189. https://doi.org/10.1007/BF00154372
Papaloizou, J., Pringle, J.E. (1978) Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables. Mon. Not. R. Astron. Soc. 182:423–442. https://doi.org/10.1093/mnras/182.3.423
Parker, E.N. (1988) Nanoflares and the solar X-ray corona. Astrophys. J. 330:474–479. https://ui.adsabs.harvard.edu/abs/1988ApJ...330..474P
de Pontieu B., McIntosh S.W., Carlsson M., Hansteen V.H., Tarbell T.D., et al. (2007) Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind. Science 318:1574-1577. https://doi.org/10.1126/science.1151747
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P. (2007) Numerical Recipes: The Art of Scientific Computing (3rd edition). Cambridge University Press, United Kingdom. ISBN 9780521880688
Ramesh, K.B. (2010) Coronal mass ejections and sunspot-solar cycle perspective. Astrophys. J. Lett. 712(1). https://doi.org/10.1088/2041-8205/712/1/L77
Rieger, E. (1989) Solar Flares — High-Energy Radiation and Particles. Sol. Phys. 121(1-2):323-345. https://ui.adsabs.harvard.edu/abs/1989SoPh..121..323R
Rieger, E., Share, G.H., Forrest, D.J., Kanbach, G., Reppin, C., Chupp, E.L. (1984) A 154-day periodicity in the occurrence of hard solar flares? Nature 312:623–625. https://doi.org/10.1038/312623a0
Robson J.D., Dodds C.J., Macvean D.B., Paling, V.R. (1971) Vibration Theory I: Receptance. In: Random Vibrations. International Centre for Mechanical Sciences (Courses and Lectures), Vol. 115. Springer, Vienna. https://doi.org/10.1007/978-3-7091-2734-6_4
Route, M. (2016) The discovery of solar-like activity cycles beyond the end of the main sequence? Astrophys. J. Lett. 830:L27. https://doi.org/10.3847/2041-8205/830/2/L27
Scherrer, P.H., Wilcox, J.M., Svalgaard, L., Duvall, Jr. T.L., Dittmer, P.H., Gustafson, E.K. (1977) The mean magnetic field of the Sun: Observations at Stanford. Sol. Phys. 54:353–361. https://doi.org/10.1007/BF00159925
Schwabe, H. (1844) Solar observations during 1843. Astronomische Nachrichten 20(495):233–236. https://ui.adsabs.harvard.edu/abs/1844AN.....21..233S
Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Tech. J. 27:379–423, 623–656. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
Singh, Y.P., Badruddin (2019) Study of the solar rotational period and its harmonics in solar activity, interplanetary, geomagnetic, and cosmic ray intensity indicators during solar polarity reversal periods. Sol. Phys. 294:27. https://doi.org/10.1007/s11207-019-1413-y
Smith, E.J., Marsden, R.G. (2003) Ulysses observations at solar maximum: introduction. Geophys. Res. Lett. 30:8027. https://doi.org/10.1029/2003GL018223
Solanki, S.K., Inhester, B., Schussler, M. (2006) The solar magnetic field. Rep. Prog. Phys. 69(3):563–668. https://doi.org/10.1088/0034-4885/69/3/R02
Soler, R., Terradas, J., Oliver, R., Ballester, J.L. (2021) Resonances in a coronal loop driven by torsional Alfvén waves propagating from the photosphere. Astrophys. J. 909(2):190. https://doi.org/10.3847/1538-4357/abdec5
Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., et al. (2007) Observation of Inertial Energy Cascade in Interplanetary Space Plasma. Phys. Rev. Lett. 99(11):115001. https://doi.org/10.1103/PhysRevLett.99.115001
Steeves, R.R. (1981). A statistical test for significance of peaks in the least squares spectrum. Collected Papers, Geodetic Survey, Department of Energy, Mines and Resources. Surveys and Mapping Branch, Ottawa Canada, pp. 149–166. http://www2.unb.ca/gge/Research/GRL/LSSA/Literature/Steeves1981.pdf
Stenflo, J., Vogel, M. (1986) Global resonances in the evolution of solar magnetic fields. Nature 319:285–290. https://doi.org/10.1038/319285a0
Srivastava, A., Shetye, J., Murawski, K., Doyle, J.G., Stangalini, M., et al. (2017) High-frequency torsional Alfvén waves as an energy source for coronal heating. Sci. Rep. 7:43147. https://doi.org/10.1038/srep43147
Taylor, J., Hamilton, S. (1972) Some tests of the Vaníček Method of spectral analysis. Astrophys. Space Sci. 17:357–367. https://doi.org/10.1007/BF00642907
Thomas, S.R., Owens, M.J., Lockwood, M. (2014) The 22-year Hale Cycle in cosmic ray flux: evidence for direct heliospheric modulation. Sol. Phys. 289(1):407–421. https://doi.org/10.1007/s11207-013-0341-5
Thomson, D., Maclennan, C., Lanzerotti, L. (1995) Propagation of solar oscillations through the interplanetary medium. Nature 376:139–144. https://doi.org/10.1038/376139a0
Tokumaru, M., Fujiki, K., Iju, T. (2015) North-south asymmetry in global distribution of the solar wind speed during 1985–2013. J. Geophys. Res. Space Phys. 120:3283–3296. https://doi.org/10.1002/2014JA020765
Triana, S.A., Dumberry, M., Cébron, D. et al. (2022) Core eigenmodes and their impact on the Earth’s Rotation. Surv. Geophys. 43:107–148. https://doi.org/10.1007/s10712-021-09668-y
Vaníček, P. (1969) Approximate spectral analysis by least-squares fit. Astrophys. Space Sci. 4(4):387–391. https://doi.org/10.1007/BF00651344
Vaníček, P. (1971) Further development and properties of the spectral analysis by least-squares fit. Astrophys. Space Sci. 12(1):10–33. https://doi.org/10.1007/BF00656134
Vecchio, A., Carbone, V. (2009) Spatio-temporal analysis of solar activity: main periodicities and period length variations. Astron. Astrophys. 502(3):981–987. https://doi.org/10.1051/0004-6361/200811024
Verscharen, D., Klein, K.G., Maruca, B.A. (2019) The multi-scale nature of the solar wind. Living Rev. Sol. Phys. 16:5, pp.136. https://doi.org/10.1007/s41116-019-0021-0
Wells, D.E., Vaníček, P., Pagiatakis, S. (1985) Least squares spectral analysis revisited. Department of Geodesy & Geomatics Engineering Technical Report 84, University of New Brunswick, Canada. http://www2.unb.ca/gge/Pubs/TR84.pdf
Withbroe, G.L., Noyes, R.W. (1977) Mass and Energy Flow in the Solar Chromosphere and Corona. Ann. Rev. Astron. Astrophys. 15(1):363–387. https://doi.org/10.1146/annurev.aa.15.090177.002051
Wolff, C.L., Blizard, J.B. (1986) Properties of r-modes in the Sun. Sol. Phys. 105:1–15. https://doi.org/10.1007/BF00156371
Zaqarashvili, T.V., Carbonell, M., Oliver, R., Ballester, J.L. (2010) Magnetic Rossby waves in the solar tachocline and Rieger-type periodicities. Astrophys. J. 709(2):749–758. https://doi.org/10.1088/0004-637X/709/2/749
Zhang, H., Huang, L., Li, X., Jiang, L., Yang, D., Zhang, F., Miao, J. (2020) Spectrum Analysis of a Coaxial Dual-Rotor System with Coupling Misalignment. Shock and Vibration 2020:5856341. https://doi.org/10.1155/2020/5856341
Zhou, W.-X., Sornette, D. (2001) Statistical significance of periodicity and log-periodicity with heavy-tailed correlated noise. Int. J. Modern Phys. C 13(2):137–169. https://doi.org/10.1142/S0129183102003024