Earth body resonance
Article Sidebar
Vols. 1-18 (1924-1944), ISSN 0044-2801
Main Article Content
Abstract
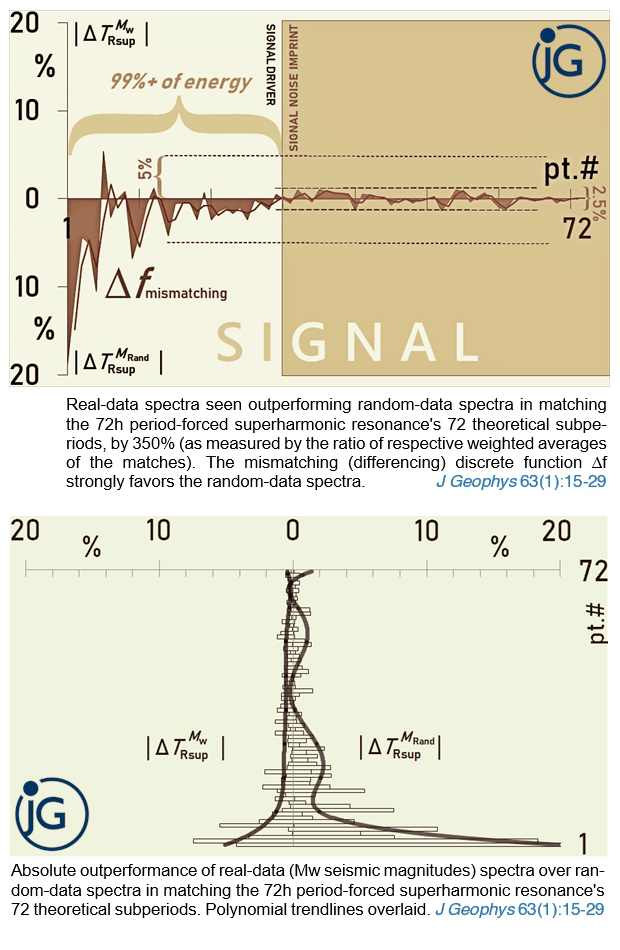
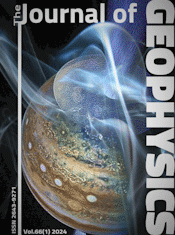
The full range of 72h-forced, 72 superharmonic resonance periods, is detected in time-series of all 866 earthquakes of (robust averages of) Mw5.6+ from USGS, EMSC, and GFZ, 2015-2019 catalogs. The resonance is in the 55’–15 days long-periodic band (0.303 mHz–0.771605 μHz) at 99–67% confidence. Moreover, omitting of the 21 overrepresenting events has improved the result. The signal is clear, strong, and stable – demonstrating beyond doubt that Mw6.2+ seismicity arises due to long-periodic resonance. Remarkably, the natural mode’s cluster was detected too; it averaged 60.1’, while the overall strongest resonance period was also 59.9’, at 2.3 var%, or to within the 1Hz sampling rate – revealing that the 72 h forcer is the modulator of the Earth’s natural period via synchronization. The dominance property of the forcer also follows from detection of its many other fractional multiples: 14/5, 3/2, 5/12, 5/36, etc. After Schumann resonance discovery in the short band (extremely long band of the EM Spectrum), this is the second report ever of a full resonance bundle in any global data, and the first ever in tectonic earthquakes occurrences. The Mw6.2+ seismotectonics arises via resonance-rupture response of tectonic plates and regions to the resonant phase or its fractional multiples. Fundamental questions of geophysics including earthquake prediction can be solved if the Earth is taken to be a multi-oscillator nonlinear system. As an immediate benefit, the find enables a reliable partial seismic anti-forecasting (prediction of seismic quiescence), months ahead globally. This discovery of mechanically induced extreme-band energy on Earth invalidates the main (heat-transfer) geophysical hypothesis and thus should drastically diminish the role of chemistry in geosciences, specifically of geochemistry.
ARK: https://n2t.net/ark:/88439/x020219
Permalink: https://geophysicsjournal.com/article/31
DOI:10.5281/2646487 | online first: 18 Apr 2019 CERN
Moon body resonance, 63(1):30-42
Detection and mapping of Earth body resonances with continuous GPS. J. Geophys. 64(1):12-33
Read the press release for this article
Article Details
References
Brunton, S.L., Proctor, J.L., Kutz, J.N. (2016) Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. (PNAS) 113(15):3932-3937
Den Hartog, J. (1985). Mechanical Vibrations (4th Ed.) Dover Publications, New York
Dziewonski, A.M., Chou, T.‐A., Woodhouse, J.H. (1981) Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. - Solid Earth 86(B4):2825-2852
Elghadamsi, F.E., Mohraz, B., Lee, C.T., Moayyad, P. (1988) Time-dependent power spectral density of earthquake ground motion. Soil Dyn. Earthq. Eng. 7(1):15-21
Grannan, A.M., Favier, B., Le Bars, M., Aurnou, J.M. (2017) Tidally forced turbulence in planetary interiors. Geophys. J. Int. 208:1690–1703
Harris, R. (1998) The Loma Prieta, California, Earthquake of October 17, 1989 – Forecasts. U.S. Geol. Survey, Washington DC
Harrison, C. (2016) The present-day number of tectonic plates. Earth Planets Space 68:37-51
Kanamori, H. (1977) The energy release in great earthquakes. J. Geophys. Res. - Solid Earth Planets 82(20):2981-2987
Kuramoto, Y. (1975) Self-entrainment of a population of coupled non-linear oscillators. (H. Araki, Ed.) Lect. Not. Phys. 39:420-422
Muller, H. (2018) Quantum Gravity Aspects of Global Scaling and the Seismic Profile of the Earth. Prog. Phys. 14(1):41-45
Nishida, K. (2014) Source spectra of seismic hum. Geophys. J. Int. 199:416–429
Omerbashich, M. (2004) Earth-model discrimination method. ProQuest, Ann Arbor, Michigan USA
Omerbashich, M. (2006a) Springtide-induced magnification of Earth mantle’s resonance causes tectonics and conceals universality of physics at all scales. Arxiv, New York City NY, USA. Retrieved from http://de.arxiv.org/abs/physics/0608026
Omerbashich, M. (2006b) Gauss-Vaníček Spectral Analysis of the Sepkoski Compendium: No New Life Cycles. Comp. Sci. Eng. 8:26-30
Omerbashich, M. (2007) Magnification of mantle resonance as a cause of tectonics. Geod. Acta 20(6):369-383
Omerbashich, M. (2008) Scale invariability. Arxiv, New York NY, USA. Retrieved from http://de.arxiv.org/abs/0801.0876
Omerbashich, M. (2016) Astrophysical cause of tectonics. (C. Yuntai, Ed.) Earthq. Sci. (In press)
Omerbashich, M. (2019) On solar origin of alleged mass-extinction periods in records of natural data. (A. Y. Rozanov, Ed.) Paleontol. J. (In press)
Pikovsky, A., Rosenblum, M., Kurths, J. (2001) Synchronization: A Universal Concept in Nonlinear Sciences (Vol. 12). Cambridge, United Kingdom: Cambridge University Press
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P. (2007) Numerical Recipes: The Art of Scientific Computing (3rd Ed.). London, United Kingdom: Cambridge University Press
Sauret, A., Le Bars, M., Le Gal, P. (2014) Tide-driven shear instability in planetary liquid cores. Geophys. Res. Lett. 41 (17):6078–6083
Schroeder, W., Treder, H.J. (1997) Einstein and geophysics: Valuable contributions warrant a second look. EOS Trans. AGU 43 (78):479–485
Stevenson, D. (2010) Planetary Magnetic Fields: Achievements and Prospects. Space Sci. Rev. 152:651–664
Tesla, N. (1919) The magnifying transmitter. Electrical Experimenter VII (74):112-113, 148, 173, 176-178
Thévenin, J., Romanelli, M., Vallet, M., Brunel, M., Erneux, T. (2011) Resonance Assisted Synchronization of Coupled Oscillators: Frequency Locking without Phase Locking. Phys. Rev. Lett. 107:104101-1-5
Vaníček, P. (1969) Approximate Spectral Analysis by Least-Squares Fit. Astrophys. Space Sci. 4(4):387–391
Vaníček, P. (1971) Further Development and Properties of the Spectral Analysis by Least-Squares Fit. Astrophys. Space Sci. 12(1):10–33
Wyss, M., Dmowska, R. (1997) Earthquake prediction – state of the art. Pure Appl. Geophys. (PAGEOPH) 149(1):350
Yang, J.H., Sanjuán, M.A.F., Liu, H.G. (2016) Vibrational subharmonic and superharmonic resonances. Comm. Nonlin. Sci. Num. Sim. 30(1-3):362–372